Play, Learn, Conquer: The Journey to a Self-Improving Game AI
Mastering Gomoku (Five-in-a-Row) and Othello with the AlphaZero Algorithm in PyTorch through Self-Play.
When we were kids, most of us might have played some board games like Go or chess. Back then, few believed AI could ever compete with humans in such deep-strategy contests. Yet thanks to breakthroughs in hardware and machine learning, AI now goes head-to-head with (or even defeats) the world’s best players in Go, chess, and more. This milestone shows how machines have learned to think several moves ahead and plan over the long term.
Imagine a board game as an arena governed by clear rules and a fixed grid. Each move not only changes the board but also spawns a whole tree of future possibilities — every response opens up another set of options, and each of those leads to yet more. In a tiny game like tic-tac-toe, that tree is small enough to fully explore, so you can brute-force every move and guarantee at least a draw.
However, in larger games such as Go or chess, the search tree explodes. In a 19×19 Go game, each player faces roughly 250 legal moves per turn, and a full game takes about 150 moves — resulting in on the order of 250¹⁵⁰ possible trajectories, far beyond brute-force reach.
To break through this computational wall, researchers turned to reinforcement learning algorithms. In 2016, DeepMind’s AlphaGo fused policy and value networks with Monte Carlo Tree Search: it first learned from human pro games via supervised learning, then sharpened itself with self-play RL to beat Lee Sedol (world champion at that time ) 4–1.
A year later, AlphaGo Zero went further — starting from pure random play and no human data, a single ResNet learned both move selection and position evaluation entirely by self-play + MCTS, and in just days it surpassed every previous AlphaGo model. In this article, I’ll cover the basics of Monte Carlo Tree Search (MCTS) and Alpha Zero algorithm, and show you how to apply them to Gomoku and Othello.
Monte Carlo Tree Search
In board games, we choose the next move by weighing the current position against possible opponent responses, aiming to maximise both immediate and future rewards. However, as I mentioned earlier, when the board becomes larger and more complex, the number of possible moves explodes and brute-force search quickly becomes impractical.
A common way to tackle this challenge is Monte Carlo Tree Search (MCTS). Instead of exhaustively expanding every branch, MCTS runs randomised simulations — called playouts — only along the most promising or under-explored branches, giving a reliable win-rate estimate without expanding every subtree.
It also apply the UCT formula to balances exploration (trying out less-visited moves) with exploitation (focusing on high-win-rate moves), so computation is concentrated where it will have the greatest impact.
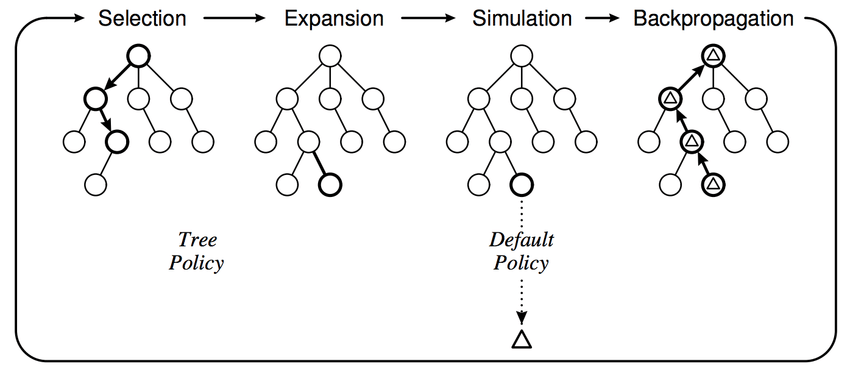
MCTS can be briefly divided into four processes: Selection, Expansion, Simulation, and Backpropagation. I will use Tic Tac Toe as an example to explain how it applies. To visualise the MCTS process, you can also try this web GUI: link.
Upper Confidence Bound for Tree (UCT)
UCT picks each child by combining the average reward (left) with an exploration term (right), so MCTS consistently balances exploiting high-value moves and exploring less-visited branches.
Q(s, a): average reward, Q = W / N
N(s): how many times state ‘s’ has been visited.
N(s, a): how many times action ‘a’ was tried from ‘s’.
P(s, a): probability of taking move ‘a’ (prior)
c is a constant that balances exploration versus exploitation.
Selection
At the beginning, set the current game board as the root node. Each node represents a unique game state; no children exist initially.
From the root, repeatedly select the action ‘a’ that maximises UCT and move to the corresponding child node
Stop until reaching a node that is not fully expanded (i.e., has at least one untried legal move).
Now, let’s try to compute the UCT for node ‘A’. First, its average reward Q = 0.75 (as 3 wins out of 4 visits). Then we add an exploration bonus, which is the square root of ln(20) over 4 (since the parent has been visited 20 times and ‘A’ itself 4 times). By setting the prior ‘P’ and exploration constant ‘c’ to 1, the final UCT score for node ‘A’ is 0.75 + 0.866 = 1.616.
Note: In the selection phase, the player switches at each level (for example, if it’s X’s turn in state A, then it’s O’s turn in state A1), ensuring that each node correctly represents whose turn it is when evaluating and back propagating values.
Expansion
If the selected node corresponds to a non-terminal state with untried moves, expand by adding one new child node:
Pick one empty cell (legal move) that hasn’t been expanded yet.
Create a child node representing the board after placing the current player’s move in that cell.
Initialise visit count N(⋅) = 0 and total value W(⋅) = 0 for the new child.
Simulation (Rollout)
From the newly added node (or from a terminal node if already expanded), play a random game until it ends:
Alternate turns between both player.
At each step, choose one of the remaining empty cells uniformly at random.
Continue until one player wins or the board is full (draw).
Record the result as the reward z = 1 if the simulated game ends in a win for the player who just moved at the expanded node, -1 if the opponent wins, else 0 (draw). For example, starting from leaf node ‘A1a’, you simulate until the game’s end and then record ‘z’ for ‘A1a’ based on which player wins.
Back Propagation
Propagate the simulation result ‘z’ back up the tree to the root. For each state–action (s,a) on the path:
Visit count: N(s) += 1
Total value: W(s,a) += z (or −z depending on perspective)
Below is an example of how back propagation works (assume z = +1 at node A1a). As the active player alternates at each level, the reward contribution switches sign accordingly when updating parent nodes.
MCTS Implementation
The following is an implementation of Tic-Tac-Toe game: it stores the board state, current player, and available moves.
do_move: places a mark and switches players.
game_end: checks all win lines or a full board, returning whether the game is over and who won (or 0 for a draw).
import math
import numpy as np
# Tic-Tac-Toe game state
class TicTacToe:
def __init__(self):
self.states = [0] * 9 # 0=empty, 1=X, -1=O
self.current_player = 1 # X starts
self.availables = list(range(9))
def do_move(self, move):
self.states[move] = self.current_player
self.availables.remove(move)
self.current_player *= -1 # switch player
def game_end(self):
lines = [(0,1,2),(3,4,5),(6,7,8),
(0,3,6),(1,4,7),(2,5,8),
(0,4,8),(2,4,6)]
for i, j, k in lines:
s = self.states[i] + self.states[j] + self.states[k]
if s == 3: return True, 1 # X wins
if s == -3: return True, -1 # O wins
if not self.availables:
return True, 0
return False, None def softmax(x):
e = np.exp(x - np.max(x))
return e / np.sum(e)
class TreeNode:
def __init__(self, parent=None, prior=1.0):
self.parent = parent
self.children = {} # action -> node
self.n_visits = 0
self.Q = 0.0 # mean value
self.P = prior # prior prob
def expand(self, action_priors):
for a, p in action_priors:
if a not in self.children:
self.children[a] = TreeNode(self, p)
def select(self, c_puct):
# pick child with highest UCT
return max(self.children.items(),
key=lambda act_node: act_node[1].Q +
c_puct * act_node[1].P *
math.sqrt(self.n_visits) /
(1 + act_node[1].n_visits))
def simulate(self, state):
"""
Perform a random rollout from the current state until terminal,
returning +1 if the current player at `state` wins,
-1 if they lose, or 0 for a draw.
"""
cur = state
while True:
end, winner = cur.game_end()
if end:
if winner == 0:
return 0
return 1 if winner == cur.current_player else -1
a = random.choice(cur.availables)
cur.do_move(a)
def update_recursive(self, value):
if self.parent:
self.parent.update_recursive(-value)
self.n_visits += 1
self.Q += (value - self.Q) / self.n_visits
class MCTS:
def __init__(self, policy_fn, c_puct=1.4, n_playout=1000):
self.root = TreeNode(prior=1.0)
self.policy_fn = policy_fn
self.c_puct = c_puct
self.n_playout = n_playout
def _playout(self, state):
node = self.root
# move down until leaf
while node.children:
action, node = node.select(self.c_puct)
state.do_move(action)
end, winner = state.game_end()
if not end:
action_priors, leaf_value = self.policy_fn(state)
node.expand(action_priors)
# Comment out this line when using AlphaZero (no random rollout)
leaf_value = node.simulate(state)
else:
# terminal value from current player's view
leaf_value = 0 if winner == 0 else (
1 if winner == state.current_player else -1
)
node.update_recursive(-leaf_value)
def get_move_probs(self, state, temp=1e-3):
for _ in range(self.n_playout):
cpy = TicTacToe()
# cpy = Board(state.width, state.height, state.n_in_row)
cpy.states = state.states.copy()
cpy.availables = state.availables.copy()
cpy.current_player = state.current_player
self._playout(cpy)
acts, visits = zip(*[(a, n.n_visits)
for a, n in self.root.children.items()])
probs = softmax(np.log(np.array(visits) + 1e-10) / temp)
return list(acts), probs
def update_with_move(self, last_move):
# reuse subtree after actual move
if last_move in self.root.children:
child = self.root.children[last_move]
child.parent = None
self.root = child
else:
self.root = TreeNode(prior=1.0)The _playout method contains one iteration of the MCTS process—including select, expand, simulate, and back propagation. By repeating these playouts multiple times, we could build up more accurate UCT scores to guide our next move.
The policy function returns the estimated action priors and a leaf value. For a pure MCTS model, it returns a uniform random distribution for the priors and sets the leaf value to zero. You can use the following code to player the game.
# uniform random policy
def policy_fn_uniform(state: TicTacToe):
moves = state.availables
prob = 1 / len(moves)
return [(m, prob) for m in moves], 0
def play_vs_human(c_puct=1.4, n_playout=1000):
game = TicTacToe()
mcts = MCTS(policy_fn=policy_fn_uniform, c_puct=c_puct, n_playout=n_playout)
human = 0
while human not in (1, -1):
human = int(input("Choose side: X(1) or O(-1): "))
symbols = {1:'X', -1:'O', 0:'.'}
print("Board: 0-8 positions\n")
while True:
end, winner = game.game_end()
if end:
print("Result:", "Draw" if winner==0 else f"{symbols[winner]} wins")
break
if game.current_player == human:
move = -1
while move not in game.availables:
move = int(input(f"Your move {game.availables}: "))
game.do_move(move)
mcts.update_with_move(move)
else:
print("AI thinking...")
acts, probs = mcts.get_move_probs(game)
ai_move = acts[np.argmax(probs)]
print("AI move:", ai_move)
game.do_move(ai_move)
mcts.update_with_move(ai_move)
for i in range(3): # display board
print(' '.join(symbols[game.states[3*i+j]] for j in range(3)))
print()AlphaZero
AlphaZero, introduced by DeepMind in 2017, is a general reinforcement-learning system that learns solely through self-play without any human game data. It uses a single neural network to predict both move probabilities (the policy) and state values.
Note: AlphaZero is a general version of AlphaGo Zero that can be applied to games other than Go, such as chess and shogi.
During gameplay, it employs a lightweight MCTS: instead of running many random rollouts to evaluate moves, it relies on the policy network to guide the search and on the value network to evaluate positions directly. This approach makes the search far more accurate and efficient, enabling AlphaZero to rapidly surpass human-level performance in games such as Go, chess, and shogi.
Gomuku Game Implementation
Now let’s implement AlphaZero to play a Gomoku game. The rules are simple: each player takes turns placing a stone of their colour on an empty intersection, and the first to form an unbroken line of five stones — horizontally, vertically, or diagonally — wins.
class Board:
def __init__(self, width=8, height=8, n_in_row=5):
self.width = width
self.height = height
self.n_in_row = n_in_row
self.players = [1, 2] # player IDs
self.states = {} # {move: player}
self.availables = [] # list of legal moves
self.current_player = None
self.last_move = -1
def init_board(self, start_player=0):
if self.width < self.n_in_row or self.height < self.n_in_row:
raise ValueError(f"Board must be at least {self.n_in_row} in both dimensions.")
self.current_player = self.players[start_player]
self.availables = list(range(self.width * self.height))
self.states.clear()
self.last_move = -1
def move_to_location(self, move):
"""Convert move index to (row, col)."""
return divmod(move, self.width)
def location_to_move(self, loc):
if len(loc) != 2:
return -1
move = loc[0] * self.width + loc[1]
return move if 0 <= move < self.width * self.height else -1
def current_state(self):
state = np.zeros((4, self.width, self.height))
for m, p in self.states.items():
r, c = self.move_to_location(m)
plane = 0 if p == self.current_player else 1
state[plane, r, c] = 1.0
if self.last_move >= 0:
r, c = self.move_to_location(self.last_move)
state[2, r, c] = 1.0
# plane 3 indicates which player's turn (first player → all ones on even moves)
if len(self.states) % 2 == 0:
state[3, :, :] = 1.0
return state[:, ::-1, :]
def do_move(self, move):
self.states[move] = self.current_player
self.availables.remove(move)
self.last_move = move
self.current_player = (
self.players[1] if self.current_player == self.players[0]
else self.players[0]
)
def has_a_winner(self):
if len(self.states) < 2 * self.n_in_row - 1:
return False, -1
w, h, n = self.width, self.height, self.n_in_row
for m, p in self.states.items():
r, c = divmod(m, w)
if c <= w - n and all(self.states.get(m + i, -1) == p for i in range(n)):
return True, p # horizontal
if r <= h - n and all(self.states.get(m + i * w, -1) == p for i in range(n)):
return True, p # vertical
if r <= h - n and c <= w - n and all(self.states.get(m + i * (w + 1), -1) == p for i in range(n)):
return True, p # diag down-right
if r <= h - n and c >= n - 1 and all(self.states.get(m + i * (w - 1), -1) == p for i in range(n)):
return True, p # diag down-left
return False, -1
def game_end(self):
win, winner = self.has_a_winner()
if win:
return True, winner
if not self.availables:
return True, -1 # draw
return False, -1
def get_current_player(self):
return self.current_player
def graphic(self):
lines = []
for i in range(self.height - 1, -1, -1):
row = []
for j in range(self.width):
move = i * self.width + j
p = self.states.get(move, -1)
if p == self.players[0]: row.append('X')
elif p == self.players[1]: row.append('O')
else: row.append('.')
lines.append(' '.join(row))
return "\n".join(lines)
def __str__(self):
return self.graphic()Note: I strongly recommend starting with a 6×6 board and n_in_row = 4, as it converges much faster than an 8×8 board.
By default this environment uses an 8×8 board with n_in_row = 5 (you can tweak both to try other setups). The neural network takes a NumPy array of shape (batch, 4, width, height) as input, where each board is split into four channels:
Channel 0: current player’s stones
Channel 1: opponent’s stones
Channel 2: a mark on the last move
Channel 3: a constant plane set to 1 if it’s player 1’s turn
This compact 4-channel encoding fully captures the game state for the network. (Note: to visualise the board, you can call the graphic() function)
Different between MCTS & AlphaZero
Classic MCTS uses random rollouts to evaluate leaf nodes and manually sets prior probabilities, but AlphaZero swaps both for a single neural network: its value head instantly estimates a position’s value and its policy head provides move priors.
We can reuse the same MCTS framework — just replace full-game simulations with the value head and handcrafted priors ‘P’ with the policy head — to achieve far stronger play with fewer playouts.
class ResidualBlock(nn.Module):
""" 2-layer residual block."""
def __init__(self, channels):
super().__init__()
self.net = nn.Sequential(
nn.Conv2d(channels, channels, 3, padding=1, bias=False),
nn.GroupNorm(4, channels),
nn.ReLU(inplace=True),
nn.Conv2d(channels, channels, 3, padding=1, bias=False),
nn.GroupNorm(4, channels)
)
def forward(self, x):
return F.relu(self.net(x) + x)
class AlphaNet(nn.Module):
"""
In: (B, 4, H, W)
Out: policy log-probs (B, H*W), value (B,)
"""
def __init__(self, width=8, height=8):
super().__init__()
self.stem = nn.Sequential(
nn.Conv2d(4, 128, 3, padding=1, bias=False),
nn.GroupNorm(4, 128),
nn.ReLU(inplace=True),
*([ResidualBlock(128)] * 4)
)
# policy head
self.policy = nn.Sequential(
nn.Conv2d(128, 2, 1, bias=False),
nn.GroupNorm(2, 2),
nn.ReLU(inplace=True),
nn.Flatten(),
nn.Linear(2 * width * height, width * height),
nn.LogSoftmax(dim=1)
)
# value head
self.value = nn.Sequential(
nn.Conv2d(128, 1, 1, bias=False),
nn.GroupNorm(1, 1),
nn.ReLU(inplace=True),
nn.Flatten(),
nn.Linear(width * height, 128),
nn.ReLU(inplace=True),
nn.Linear(128, 1),
nn.Tanh()
)
def forward(self, x):
out = self.stem(x)
policy = self.policy(out)
value = self.value(out).view(-1)
return policy, valueSelf Game Play & Dirichlet Distribution
To collect training data, we let the model play against itself in self-play, recording each trajectory as (state, prior, reward). However, pure self-play can quickly converge on a narrow set of moves and risk overfitting its own strategy.
To maintain exploration, AlphaZero injects Dirichlet noise into the root-node priors — mixing network-generated probabilities with random samples — so the search stays diverse and uncovers stronger lines over time.
def policy_value_fn(board, net):
state = board.current_state()[None, ...] # (1,4,w,h)
state_tensor = torch.from_numpy(state).float().to(next(net.parameters()).device)
net.eval()
with torch.no_grad():
log_probs, value = net(state_tensor)
probs = np.exp(log_probs.cpu().numpy().flatten())
action_priors = [(m, probs[m]) for m in board.availables]
return action_priors, value.item()
def start_self_play(net, board_width, board_height, n_in_row,
playouts, c_puct, temp=1e-3):
board = Board(board_width, board_height, n_in_row)
board.init_board()
mcts = MCTS(policy_fn=lambda b: policy_value_fn(b, net),
c_puct=c_puct, n_playout=playouts)
states, mcts_probs, players = [], [], []
while True:
acts, probs = mcts.get_move_probs(board, temp)
prob_array = np.zeros(board.width * board.height)
prob_array[list(acts)] = probs
# Apply Dirichlet Noise
noise = np.random.dirichlet([0.3] * len(probs))
move = np.random.choice(acts, p=0.75 * probs + 0.25 * noise)
states.append(board.current_state())
mcts_probs.append(prob_array)
players.append(board.get_current_player())
board.do_move(move)
mcts.update_with_move(move)
end, winner = board.game_end()
if end:
# Compute Z: win +1, lose -1, draw 0
z = np.zeros(len(players))
if winner != -1:
z = np.where(np.array(players) == winner, 1.0, -1.0)
mcts.reset()
return winner, list(zip(states, mcts_probs, z))We can also accelerate the data-collection process by running the environment in parallel — for example, if your machine has 12 CPU cores, you could launch 12 workers to gather data simultaneously.
def _self_play_worker(net_state, board_cfg, playouts, c_puct, temp):
net = AlphaNet(board_cfg["w"], board_cfg["h"]).cpu()
net.load_state_dict(net_state)
winner, play_data = start_self_play(
net,
board_width=board_cfg["w"],
board_height=board_cfg["h"],
n_in_row=board_cfg["n"],
playouts=playouts,
c_puct=c_puct,
temp=temp
)
return winner, play_data
from joblib import Parallel, delayed
def collect_selfplay_data(net, data_buffer, board_cfg, playouts, c_puct, temp=1.0, n_games=12):
net_state = {k: v.cpu() for k, v in net.state_dict().items()} # Move weight to cpu
args_list = [
(net_state, board_cfg, playouts, c_puct, temp)
for _ in range(n_games)
]
results = Parallel(n_jobs=n_games, backend="loky")(delayed(_self_play_worker)(*args) for args in args_list)
for winner, play_data in results:
for state, mcts_prob, z in play_data:
data_buffer.append((state, mcts_prob, z))During training, we will use separate losses for each head: v_loss is the MSE between the predicted value and the actual game outcome, and p_loss is the cross-entropy between the predicted and target priors to maximise log-likelihood.
def train_step(net, optimizer, scheduler, scaler, device, loader, epochs):
net.train()
data_iter = iter(loader)
total_loss, total_entropy = 0.0, 0.0
for _ in range(epochs):
try:
state_b, prob_b, winner_b = next(data_iter)
except StopIteration:
data_iter = iter(loader)
state_b, prob_b, winner_b = next(data_iter)
state_b = state_b.float().to(device)
prob_b = prob_b.float().to(device)
winner_b= winner_b.float().to(device)
optimizer.zero_grad()
with torch.amp.autocast(device_type=device.type):
log_probs, value = net(state_b)
v_loss = F.mse_loss(value.view(-1), winner_b)
p_loss = -torch.mean((prob_b * log_probs).sum(dim=1))
loss = v_loss + p_loss
if scaler: # mixed precision
scaler.scale(loss).backward()
scaler.unscale_(optimizer)
torch.nn.utils.clip_grad_norm_(net.parameters(), max_norm=1.0)
scaler.step(optimizer)
scaler.update()
else:
loss.backward()
torch.nn.utils.clip_grad_norm_(net.parameters(), max_norm=1.0)
optimizer.step()
entropy = -torch.mean((torch.exp(log_probs) * log_probs).sum(dim=1))
total_loss += loss.item()
total_entropy += entropy.item()
scheduler.step()
return total_loss / epochs, total_entropy / epochsTraining Loop & Tips for AlphaZero
Finally, here is the main training loop. It will take around 12 hours to train on a Colab L4 GPU. To further improve the model’s performance, here are some tips you can try:
Dynamic playout budget: start with fewer MCTS playouts per move in early training and ramp up as the network strengthens — focus compute where it helps most.
Adaptive c_puct: decay your exploration constant over time so you explore heavily at first, then shift toward exploitation as policy/value accuracy improves.
Pure MCTS benchmark: periodically play your trained network against a pure-MCTS (no neural net) opponent to directly measure the model’s strategic strength.
Temperature annealing: start self-play with a higher action-sampling temperature (e.g. 1.0) and gradually lower it toward 0.1 as training progresses to sharpen your policy.
import os
import math
import random
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import matplotlib.pyplot as plt
from torch.utils.data import DataLoader
from collections import deque
from joblib import Parallel, delayed
output_dir = 'Put your dir here'
os.makedirs(output_dir, exist_ok=True)
c_puct = 3
epochs = 3
playouts = 200
batch_size = 256
learn_rate = 1e-3
buffer_size = 5000
num_iterations = 2000
loss_history = []
board_cfg = {'w': 6, 'h': 6, 'n': 4}
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
net = AlphaNet(board_cfg["w"], board_cfg["h"]).to(device)
optimizer = torch.optim.Adam(net.parameters(), lr=learn_rate, weight_decay=1e-4)
scheduler = torch.optim.lr_scheduler.MultiStepLR(optimizer, milestones=[500, 1000], gamma=0.5)
scaler = torch.amp.GradScaler('cuda')
data_buffer = deque(maxlen=buffer_size)
for it in range(1, num_iterations + 1):
collect_selfplay_data(net, data_buffer, board_cfg,
playouts, c_puct, temp=1.0)
if len(data_buffer) < batch_size:
continue
loader = DataLoader(list(data_buffer), batch_size=batch_size, shuffle=True)
loss, entropy = train_step(net, optimizer, scheduler, scaler, device, loader, epochs)
if loss is not None:
loss_history.append(loss)
if it % 200 == 0:
snap_path = os.path.join(output_dir, f"snapshot_it{it}.pth")
torch.save(net.state_dict(), snap_path)
print(f"[Iter {it}] Snapshot saved to {snap_path}; Loss = {loss}")
print("Training finished!")You can use the following code to play against the AI. Note that you can choose a relatively large n_playout during inference; this allows the model to evaluate more future steps and further increase its win rate.
Note: using a lower temperature (e.g., 0.001) will sharply peak the action probability distribution, making the move selection nearly deterministic
def human_vs_ai(model_path, board_width=6, board_height=6,\
n_in_row=4, c_puct=3, n_playout=500):
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
net = AlphaNet(board_width, board_height).to(device)
net.load_state_dict(torch.load(model_path, map_location=device))
net.eval()
board = Board(board_width, board_height, n_in_row)
board.init_board(start_player=0)
mcts = MCTS(lambda b: policy_value_fn(b, net), c_puct=c_puct, n_playout=n_playout)
while True:
print("\nCurrent board:")
print(board.graphic())
end, winner = board.game_end()
if end:
if winner == -1:
print("Game over: Draw") # -1 indicates no winner
else:
print(f"Game over: Player {winner} wins!")
break
# Human player's turn
if board.get_current_player() == board.players[0]:
while True:
try:
# Prompt user for move input in "row,col" format
raw = input("Enter your move (row,col), e.g. 2,3: ")
row, col = map(int, raw.strip().split(','))
move = board.location_to_move((row, col))
if move in board.availables:
break
else:
print("That position is not available. Try again.")
except Exception:
print("Invalid input format. Please enter two integers as 'row,col'.")
board.do_move(move)
mcts.update_with_move(move)
# AI player's turn
else:
# Get move probabilities from MCTS
# Choose move with highest probability
acts, probs = mcts.get_move_probs(board, temp=1e-3)
move = acts[np.argmax(probs)]
print(f"AI chooses move: {board.move_to_location(move)}")
board.do_move(move)
mcts.update_with_move(move)Practice: Othello and Other Board Games
In this article, I introduced how to leverage Monte Carlo Tree Search (MCTS) to play tic-tac-toe and built an AlphaZero agent for Gomoku. But the power of AlphaZero is not limited to these games; in fact, any board game that can be expressed as a grid of states — whether it’s Othello (Reversi), Checkers, Chess, or even more exotic turn-based contests — can be tackled with the same neural-network and MCTS framework.
By setting up the game environment and redefining the model’s input/output representation, you can repurpose this general algorithm for new games in just a few lines of code. Here are some game environment you can try to implement:
OpenAI Gym — Classic control and board-game environments (e.g. Tic-Tac-Toe, Connect Four).
PettingZoo — A wide range of multi-agent environments, including many turn-based games.
RLCard — Specialised for card and board games (e.g. Blackjack, Uno, Mahjong).
OpenSpiel — DeepMind’s collection of environments for general game-playing research.
Finally, I hope you enjoyed this article. I will write more articles related to AI, including explanations of their underlying principles and how to implement them.
If that sounds interesting to you, feel free to follow me. 👏 😁












