Mastering Game Worlds: A Deep Dive into Reinforcement Learning
Unleashing AI Potential in Gym’s Flappy Bird, Car Racing, and the Snake Game
In recent years, AI has shown impressive success in games like Go and chess, surprising many by outperforming top human players. These achievements highlight the rapid advancement of technology.
A significant advancement in this field is ‘ChatGPT’, a large language model known for its ability to understand and utilise human language.
While ChatGPT is primarily based on transformers and supervised learning techniques, it has been fine-tuned using reinforcement learning from human feedback (RLHF), demonstrating how machines can learn from their actions and improve based on their experiences.
This article will be split into two parts. In this part, we will explore some basic theories of Reinforcement Learning while playing the Flappy Bird game using the REINFORCE method with PyTorch.
In the next part, we will study more complex RL algorithms such as the Advantage Actor Critic (A2C) and the current state-of-the-art algorithm, PPO.
Reinforcement Learning
Reinforcement learning is a machine learning method that focuses on learning behavioral strategies through interactions with an environment, aiming to achieve specific goals or maximise performance metrics. It consists of three main elements: Environment, Agent, and Reward.
Agent receive state (s_t) from the Environment
Based on that state, Agent provides an action (a_t) to the Environment
The environment goes to a new state (s_t+1) and gives some reward (r_t+1) to the Agent
Environment
The environment is the system which interacts with the agent . It defines all the possible states an agent might encounter, the actions that can be taken in those states, and the outcomes of those actions.
The environment responds to the agent’s actions by providing new states and reward information, which are used to guide the agent’s learning process. The Environment defines the following information:
Action Space: defines a set of the possible actions taken by the agent
Observation Space: defines all possible states that an agent can observe. These states provide the information needed by the agent to decide its next action. The state space can be finite or infinite, and can be continuous or discrete
Reward Function: Reward Function provides an immediate evaluation (reward) of the agent’s actions, guiding the agent to learn how to adjust its strategy to obtain a higher total reward.
Transition dynamics: Transition dynamics describe the probabilities of the environment moving to a new state after a given current state and a specific action are taken.
Reinforcement learning is an art of rewards and punishments, where a well-designed environment can significantly influence model performance.
Agent
In reinforcement learning, an agent refers to an entity that can observe the environment, make decisions, and execute actions. The goal of the agent is to learn a strategy (policy), which is a method for choosing the best action in a given environmental state, in order to maximise the rewards obtained over the long term.
Reward
Reward is a key signal that guides an agent’s learning process, providing feedback on its actions. These rewards, positive or negative, help the agent understand the consequences of its actions in achieving its goal.
The primary goal for the agent is to maximise its total reward over time by learning a strategy (policy) to choose the best actions in various state.
Gt is the total reward at timestep t (also known as the return). It is defined as the sum of the rewards from timestep t to the end of the episode (T). Additionally, we apply a discount rate, γ, to each reward. This factor determines how much future rewards contribute to the total reward at timestep t.
The discount rate γ is a value between 0 and 1. Taking 0.95 as an example, the reward r_t+n expected to be received in the more distant future is multiplied by a smaller factor, 0.95^(n-1).
This is because the probability of reaching a state that far in the future is relatively lower, and consequently, the reward it provides should be smaller to be considered reasonable.
Here is a simple example of calculating the reward. The images of ‘snake’ and ‘goal’ respectively represent the initial state and the terminal state. We now have two possible paths to the goal:
Path 1: Go straight up, then left to the goal
Path 2: Go right, then up to the goal
when discount rate γ = 1
R(Path 1) = 2 + γ(-3) + γ²(0) + γ³(1) = 0
R(Path 2) = 1+ γ(0) + γ²(3) + γ³(0) = 4
We can see there are different trajectories (path) that can reach the goal, but each trajectory can lead to very different returns (0 and 4). Thus, finding the best trajectory to maximise the total reward is the goal in Reinforcement Learning (RL). 💪
Episode: An episode refers to a sequence of interactions between an agent and an environment, starting from an initial state until reaching a terminal state.
Trajectory: A trajectory, commonly represented as τ, describes a specific sequence of states, actions, and rewards experienced by an agent. For instance: τ = (s₀, a₀, r₁, s₁, a₁, r₂, s₂, a₂, …, s_T, a_T, r_T+1, s_T+1).
Most of the time, a trajectory can be seen as a subset of an episode.
Value Function
To define how well our state is, we have to have a function to determine it, which is the value function.
Essentially, this function estimates the expected return for being in that state . It gives a sense of the long-term benefit of being in a particular state, under a specific policy (a strategy that the agent follows).
The value function defined above can be reformulated into a recursive form, which enables recursive computation of the state value.
In the value function, the expected value of the transition probability P(a ,s→s′) is used to account for real-world scenarios where the outcome (state s′) of taking the same action (a) in the same state (s) may vary.
The symbol π represents the agent’s policy, where π(a | s) denotes the probability of the agent selecting action a in state s.
Now let’s do some practice ~~ 🍎
r represents the immediate reward obtained when transitioning from one state to another (e.g., transitioning from s_1 to s_3 yields a reward of 3)
In this scenario, we have four states: s1 as the starting state, and s2, s3, and s4 as the terminal states. Two actions, ‘left’ or ‘right’, can be chosen, each with its own set of transition probabilities between these states.
Value at state 1 under difference policy:
V(π = always left) = 0.5 * 2 + 0.5 * 4 = 3
V(π = always right) = 0.33 * 3 + 0.67 * 4 = 3.67
V(π = 50% left, 50% right) = 0.5 * V(left) + 0.5 * V(right) = 3.335
This example takes into account the transition probabilities (e.g., action = right: 33% to s3, 67% to s4), highlighting the stochastic nature of the transitions where the same action does not guarantee the same outcome every time.
Let’s try a more complex example ~~
For simplicity, in this example, we will ignore the transition probabilities, and the agent can only choose to perform an ‘up’ or ‘down’ action at the beginning. For subsequent states, the agent always go right.
S1 is starting state, S6 is the terminal state, terminal state value = 0
For π = always up, γ = 1
V(s6) = 0
V(s3) = V(s5) = 10 + γV(s6) = 10
V(s2) = 2+ γV(s3) = 12
V(s4) = 4+ γV(s5) = 14
V(s1) = 1 + γV(s2) = 13
For π = (50% up, 50% down), γ = 1
V(s6) = 0
V(s3) = V(s5) = 10 + γV(s6) = 10
V(s2) = 2+ γV(s3) = 12
V(s4) = 4+ γV(s5) = 14
V(s1) = (1 + γV(s2)) * 0.5 + (2 + γV(s4)) * 0.5 = 9.5
This example shows the state values under different policies. We can conclude that the first policy (“always up”) is better, as it could provide a higher value for state 1 (13 > 9.5).
Q function
In practice, if the value of all states is known, we can maximise the cumulative reward by ensuring the agent moves to the state with the highest value at each timestep.
However, since calculating the state value requires knowledge of the transition probabilities, which are usually unknown. Therefore, using the state-action function (Q function) becomes a better choice.
Since the Q value can be learned directly from experiences, there is no need to know the environment’s transition probabilities.
The Q function, or action-value function, defines the value of taking action a in state s (under policy π). Unlike the value function, which evaluates states, the Q function directly assesses the value of a chosen action, so there’s no need to account for the probability π(a∣s).
The value function could also be seen as the sum of the Q function for all possible actions a.
In a value-based approach like Q-learning, a policy that always picks the action with the highest Q value for each state s ensures automatic maximisation of the total reward.
However, when the action space is very large or continuous, calculating all possible Q-values to identify the best action for each state becomes impractical. 😢
Q*(s, a) in the above equation is the optimal Q function, For details on how to find the optimal V and Q, please refer to: link 👏 👏
Policy-Based Methods
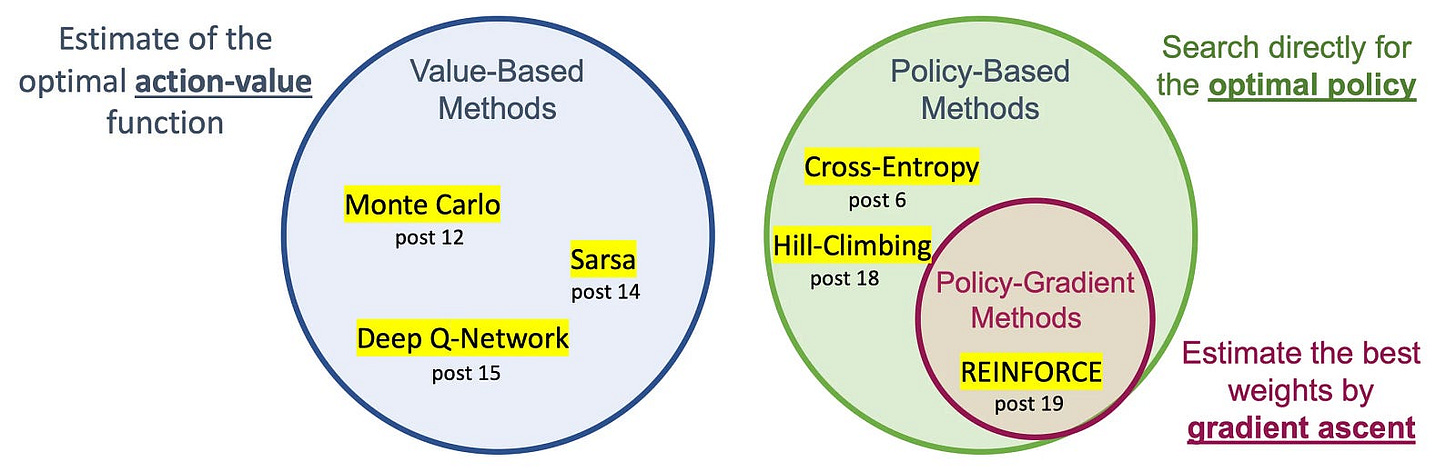
Policy-based methods in reinforcement learning, directly parameterise and optimise the policy that an agent follows to select actions, without explicitly computing value functions as intermediates (value-based methods).
The policy, denoted by π(a∣s;θ), is a function that maps states to a probability distribution over actions, where θ represents the parameters of the policy (e.g., the weights of a neural network).
REINFORCE
REINFORCE is a type of policy-gradient method that optimises a policy. It does this by estimating the gradient of the expected return with respect to the policy parameters and then adjusting those parameters using gradient descent.
The gradient scale is proportional to the return (R(τ)), which indicates the quality of the action taken. Meanwhile, the gradient itself is represented by the logarithm of the probability of taking that action.
This method seeks to increase the probability of actions that yield high return and decrease the probability of actions that result in low return.
Details of the math proof of policy gradient can be found here: link
STEP OF REINFORCE
In the REINFORCE method, it is necessary to compute the return using real samples. Additionally, a full trajectory, obtained through the Monte-Carlo method, is required for implementation.
Initialise the network with random weights.
Play N full episodes, gather their trajectory (s, a, r, s’)
calculate Return for every time step.
calculate the loss function L = -R(τ)logπ(a|s)
update the model weights
Implementation
In our first implementation, we are using the Gym environment to play the FlappyBird game.

Before we start, it is very important to understand the details of the environment. Make sure you read through the document every time before implementing.
import os
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
import gymnasium as gym
import flappy_bird_gymnasiumdef make_env(env_id):
def wrapped_env():
env = gym.make(env_id, render_mode='rgb_array')
# could add some environment wrapper
return env
return wrapped_env
env_id = 'FlappyBird-v0'
env = make_env(env_id)()
obs, _ = env.reset()
image = env.render()
plt.imshow(image)
plt.axis('off')
plt.show()The observation consists of a 1D array with 180 data points collected by a LIDAR sensor. The agent can take two possible actions: 0 for doing nothing and 1 for flapping.
You are also allowed to take the entire game screen as the observation for the model, details can refer to here.
BirdAgent & Training
class BirdPolicy(nn.Module):
def __init__(self):
super(BirdPolicy, self).__init__()
self.fc1 = nn.Linear(180, 128)
self.relu = nn.ReLU()
self.fc2 = nn.Linear(128, 2)
self.softmax = nn.Softmax(dim=-1)
def forward(self, x):
x = self.relu(self.fc1(x))
x = self.fc2(x)
return self.softmax(x)The agent is primarily responsible for making decisions based on the state provided by the environment. It returns a probability distribution representing the likelihood of selecting each possible action.
Therefore, the number of actions, denoted as n_action, equals the action space of the environment, which is 2.
Finally, here is the training loop ~~ ✋
def REINFORCE(env, episodes, policy, device, optimizer):
for episode in range(episodes):
obs, _ = env.reset()
log_probs = []
rewards = []
done = False
while not done:
# Add batch dimension
obs = torch.FloatTensor(obs).unsqueeze(0).to(device)
probs = policy(obs)
action = torch.distributions.Categorical(probs).sample()
log_prob = torch.log(probs.squeeze(0)[action])
obs, reward, done, _, info = env.step(action.item())
log_probs.append(log_prob)
rewards.append(reward)
Return = []
Gt = 0
for reward in rewards[::-1]:
# bellman equation
# computed from back to front
Gt = reward + 0.99 * Gt
Return.insert(0, Gt)
Return = torch.tensor(Return).to(device)
policy_loss = []
for log_prob, R in zip(log_probs, Return):
# compute policy gradient
policy_loss.append(-log_prob * R)
policy_loss = torch.cat(policy_loss).mean()
optimizer.zero_grad()
policy_loss.backward()
optimizer.step()
if episode % 200 == 0:
print(f'Episode {episode+1}, Total Reward: {sum(rewards)}')
torch.save(policy.state_dict(), f"./weight_epoch.pt")device = "cuda" if torch.cuda.is_available() else "cpu"
policy = BirdPolicy().to(device)
optimizer = optim.Adam(policy.parameters(), lr=1e-4)
# train for 20000 iterations
REINFORCE(env, 20000, policy, device, optimizer)Conclusion
In this article, I provide a brief introduction to the fundamental principles of reinforcement learning, including the Value function, Q function, and others. I also introduce the REINFORCE algorithm from policy gradient methods and use it to play the Flappy Bird game.
In the next part, I will introduce two other policy gradient methods, A2C and PPO, and implement them in two games: Car Racing and the Snake game.
Finally, I hope you enjoyed this article. I will write more articles related to AI, including explanations of their underlying principles and how to implement them.
If that sounds interesting to you, feel free to follow me. 👏 😁
My Medium: link
My LinkedIn: link


















